Everything You Need to Know About The Quadrivium
The quadrivium has been a research interest of mine for over 30 years. During that time, I have accumulated quite a bit of knowledge concerning the subject. The quadrivium examines the relationship between arithmetic, music, geometry, and astronomy. What makes this study special is that it does not focus on any one particular discipline. Instead, it examines the relationships between these four disciplines when they are combined. The result is a totally different understanding than one can arrive at through studying any of these disciplines separately. So instead of an understanding limited by a single discipline, a much broader and expansive understanding can be acquired.
My research is not a rehashing of traditional music theory or common musical practices. Nor is it an examination of standard arithmetic, geometric, or astronomical practices. This is my effort to educate myself as to the big picture i.e. what can be learned from studying these disciplines together, as they were meant to be when they were included in the seven liberal arts of the Middle Ages. The result is been very interesting.
The concept is ancient and was expressed by the Pythagoreans as follows:

What Are Overtones?
My introduction to this study began with an examination of the overtone series. Any musical pitch, whether produced by a musical instrument or the human voice, is not just a single pitch. It is composed of a potentially endless number of higher frequencies called overtones. These overtones can be made clearly audible, particularly by Tuvan throat singers, practitioners of harmonic chant, or practically anyone with proper training. Overtone singing is practiced by many cultures around the world.

Examples of Overtone Singing:
David Hykes, Kyrie
Amazing Grace using
throat singing
How to Master Overtones With Many Examples
research paper
My research paper, titled The Common Nature of Space and Time, was recently published by the Journal of Interdisciplinary Sciences and can be viewed or downloaded at this web address: http://journalofinterdisciplinarysciences.com/wp-content/uploads/2019/10/6-The-Common-Nature-of-Space-and-Time.pdf. Pages 2-5 of the paper briefly illustrates overtones and how the overtone series works.
The following diagram is taken from my paper, showing the first eight notes in the overtone series and the musical intervals and frequencies that correspond to those notes:

Brief Example of Geometry and the Musical Overtone Series

The geometry is uncomplicated. Take a square where all four sides are equal. Let’s say that this square has a value of 1. The diagonal of that square will be √2, the square root of 2.

That diagonal can now become the side of a new square where all four sides are equal to the diagonal of the first square. Each time the process repeats, it creates a new square that has twice the area of the preceding square! In other words, the area doubles, just like the frequency of musical octaves.
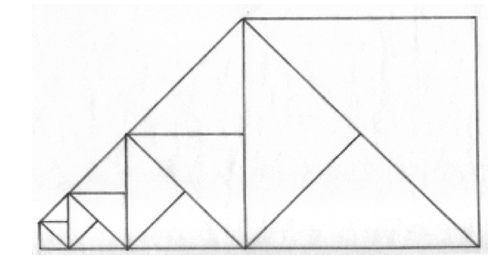
This process can be repeated, creating an endless sequence of squares that double in area.
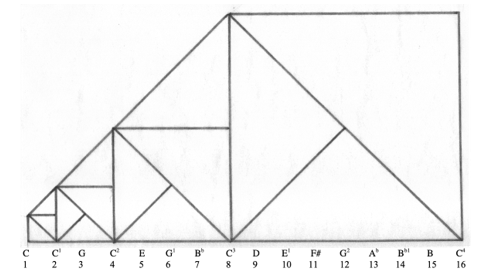
The diagram below illustrates the overtone series superimposed on the square root of 2 (√2) sequence.
Astronomy
As previously stated, the Pythagoreans held the view that astronomy is the study of number in space and time. Posted below are two links to webpages that illustrate how the musical ratios contained in the overtone series correspond to certain lunar and planetary orbits found both inside and outside of our solar system. The terms used to refer to these relationships are orbital resonance and mean-motion resonance.
Art and Geometry
In addition to lectures and presentations for advanced mathematicians and musicians, I offer an educational component for high school and junior high school students that involves geometry and art. All that is required is a compass and ruler. Posted below are a few examples of polygons I have drawn. What started out as an attempt to have a better understanding of geometry turned an artistic exercise in geometry, including all many of the polygons. These were all produced using plane geometry with only a compass and straight edge. This provides students of all ages with an opportunity to enjoy an artistic endeavor while also learning geometry.






